Plotting additional bearings to confirm a location

So far we have determined our location using a single bearing to a known feature and the knowledge that we are on the shoreline of the lake. These two pieces of information intersect in two possible places. But since we know which side of the lake we are on, and that the cabin is across the lake from our location, we know which intersection to use for our location.

What we do not know is what impact any number of possible errors might have on our location.

What could these errors be?

• Error in sighting the bearing to the cabin.
• Wrong cabin, or cabin is in the wrong place on the map.
• Water line has changed from what is shown on the map.
• Error in plotting the bearing onto the map.

The solution is to use more than the minimum amount of information required.

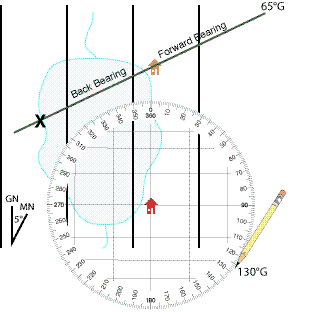
In our example we can take a bearing on a second known cabin. Doing that, our compass provides a result of 125°M or 130°G.

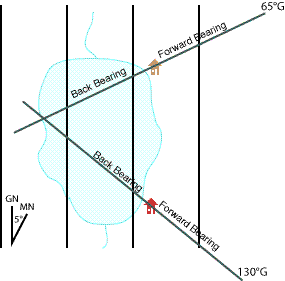
These two bearings cross near, but not exactly on the shoreline. But we know that our feet are not wet. So there is either some error in the location of the shoreline on the map, or in the bearings we have plotted. Unless we had reason to suspect the shoreline on the map, we would likely assume a bit of sighting or plotting error and adjust out position to the mapped shoreline nearest the bearing intersection.

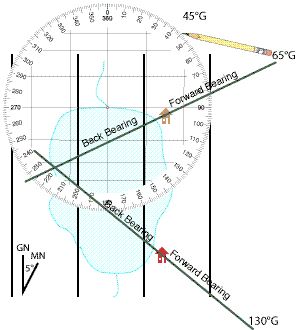
Plotting a third bearing will likely confirm if the problem is error in out sighting and plotting, or the mapped position of the shoreline. We take a sighting to the location where a stream runs into the north end of the lake and get a result of 40°M or 45°G.

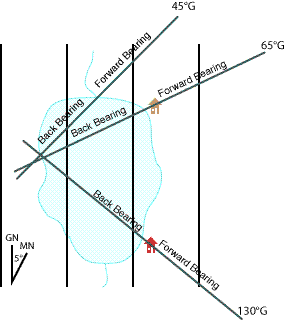
With the third bearing plotted we see that our bearings do not intersect at a single point. This is common, and indicates that there is some error in our sighting and plotting. The smaller the triangle, the smaller the errors.

The shoreline of the lake is within the small triangle formed by our bearings and is likely the best overall location to use as our current location.

Now we can locate the cave on the opposite shoreline.

In the last part of this tutorial we can use a bearing to locate a distant object. In our example this is a cave entrance we can see across the lake.